Deep neural nets provide a very specific strength: they are great function approximators. You can expand this function to all sorts of things: housing prices, language prediction, game-playing…and I am constantly being amazed at the kind of functions it can approximate as well as what it cannot.
So this week I wanted to investigate how well it approximates functions that use logic. I had been noticing that simple logic it learned readily, but suspected that layered logic was far more difficult. So I journeyed into a simple example to learn more.
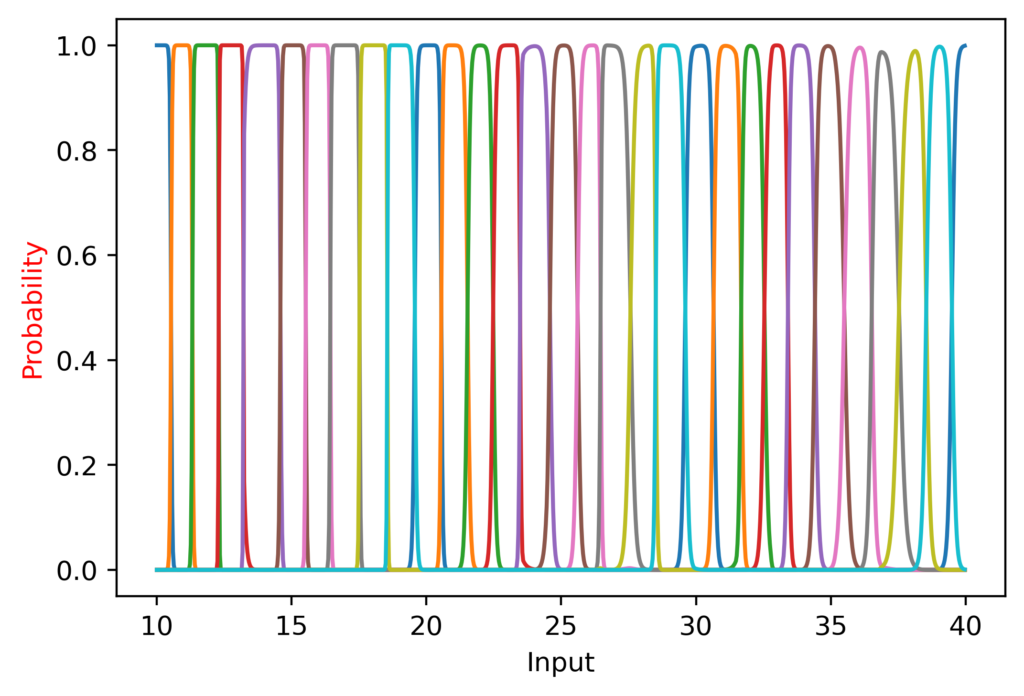
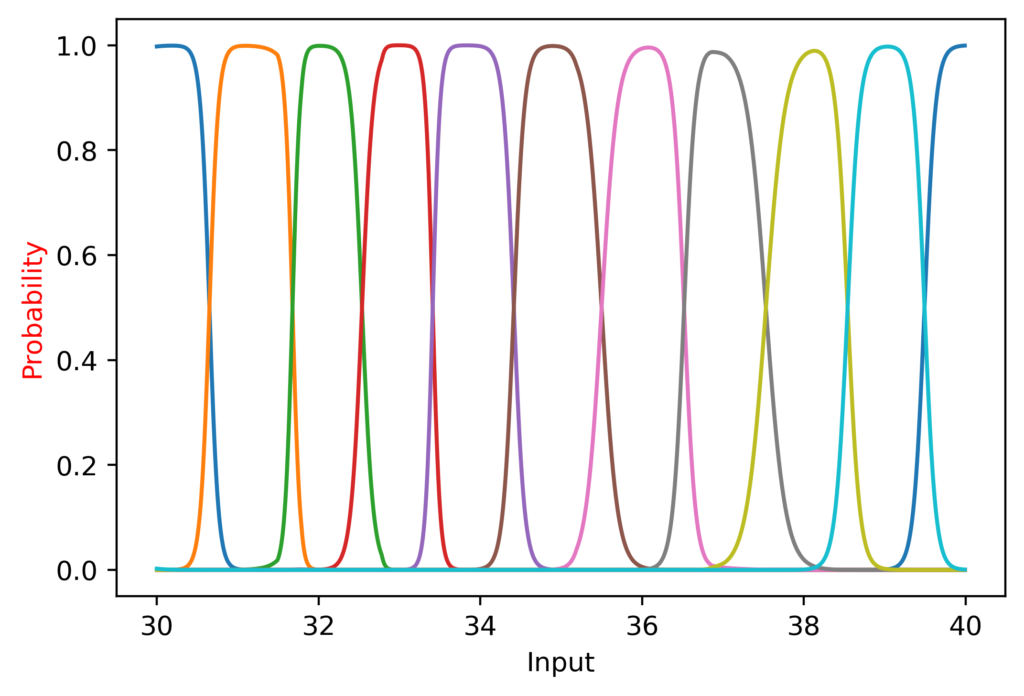
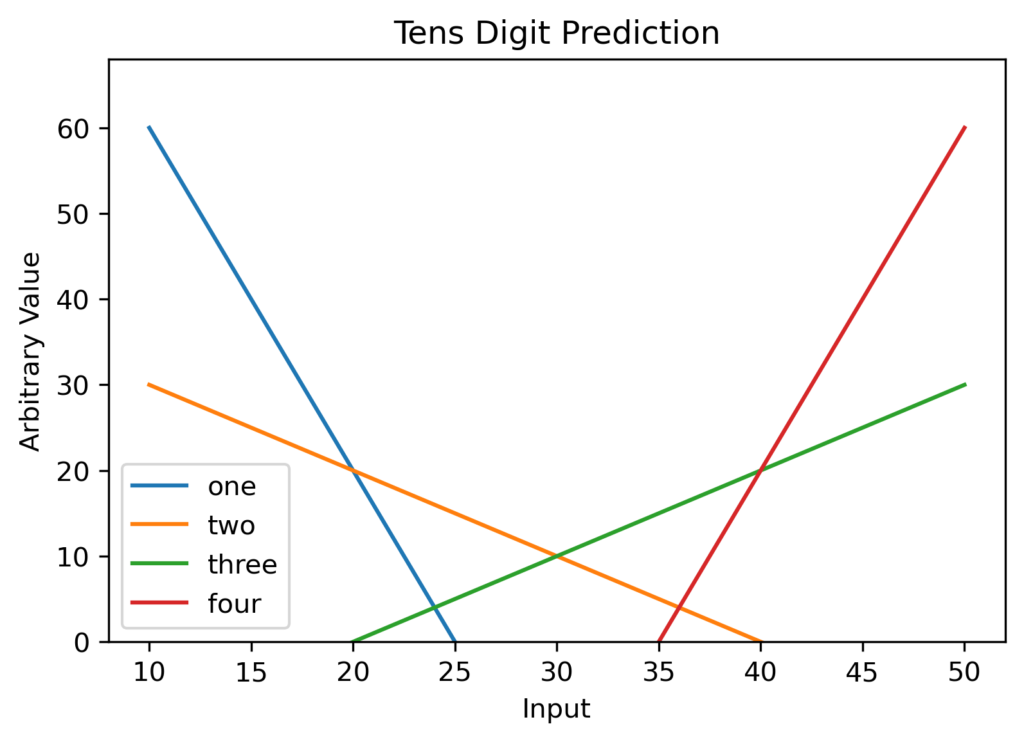
Anyway – I built a model to predict digits. No, not handwritten digits – literally just the digits of the input. Input of 247? The hundreds digit is “2”, the tens “4”, and the ones “7”. The first time, I started with data generated on the range of integers from 10 to 80, and had it end in two outputs: one for the tens digit, and one for the ones. My prediction was that it would get the tens digit with ease , as I reasoned that it is easy to fit linear lines that each are the maximum for the desired range (as in fig 1). The real interest, however, was in the one’s digit – which would have to reset every ten. I didn’t (and still don’t) believe DNN’s can estimate a sine wave, so I wasn’t quite sure what would happen.
The first thing that I learned was that I couldn’t have the final layer of my model be an argmax, even though my interest was only what the prediction was. I needed to use a softmax layer, as it plays an important role in giving the model a gradient from which to train, whereas a argmax does not tell it in which direction to move to make the model more accurate.
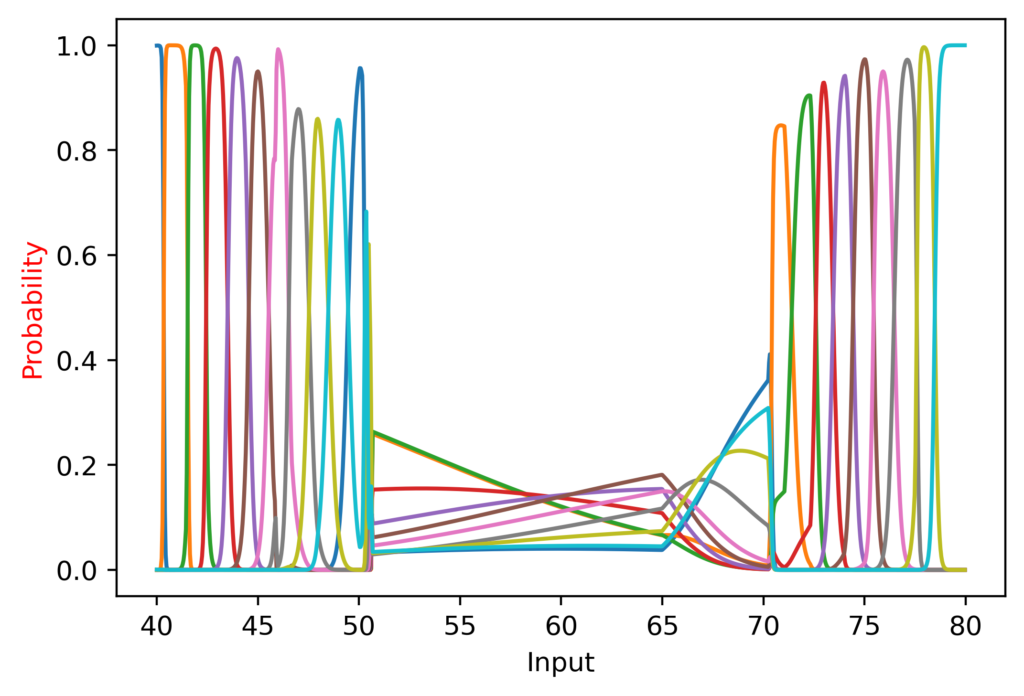
Once I sorted that, I had some preliminary results: the tens trained quickly and accurately, as predicted. However, the ones were very accurate at the start and lost accuracy as the numbers increased – until right before the end, when they suddenly gained accuracy again! This held across training a new model several times, revealing it was not a quirk of that initialization. I decided to plot it, to delve further into what was going on.
It did great from 10 to 50, suddenly took a nap, and recovered after 70!
I also noted that at the lower range the peaks were more “sharp”, since CategoricalCrossentropy (the loss function I am using) still generates a loss even if the softmax outputs a value of 0.99.
(It is worth noting here that while I am plotting the continuous function, it is not being trained on continuous data; the inputs are only integers).
Since this all seemed to be working, my next model increased the inputs to three digits. I decided to investigate several factors, to see how they related:
- The number of “Universal” layers
- The number of ones, tens, and hundreds layers
- The number of epochs trained
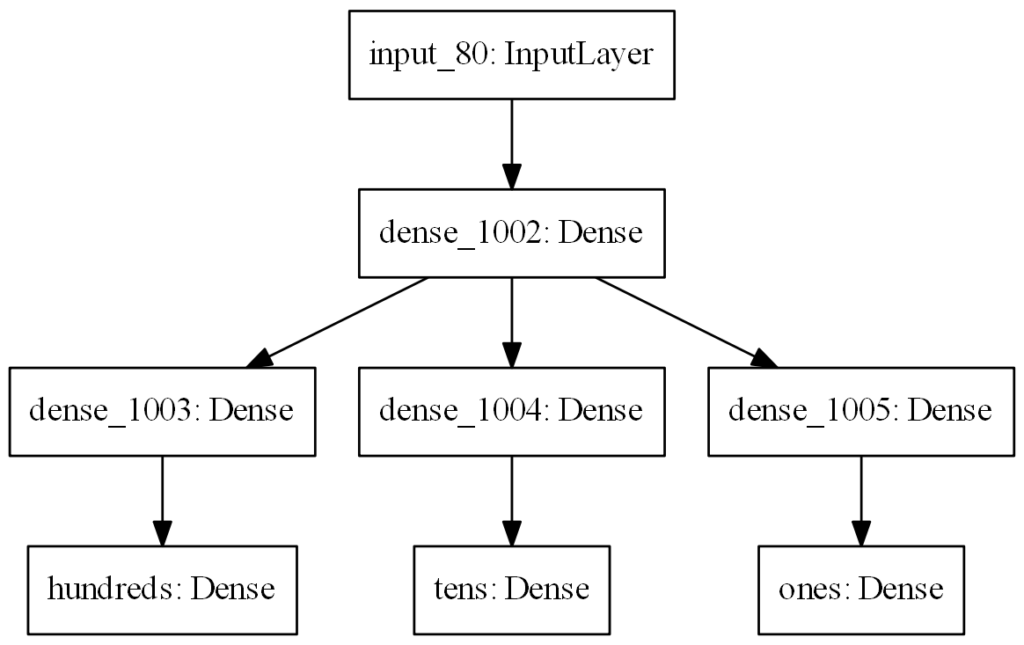
See the table and figure for the model layout and conditions. Since the number of ones, tens, and hundreds layers don’t affect each other, their interactions were not investigated.
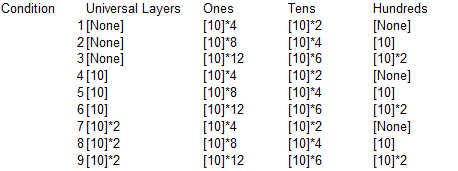
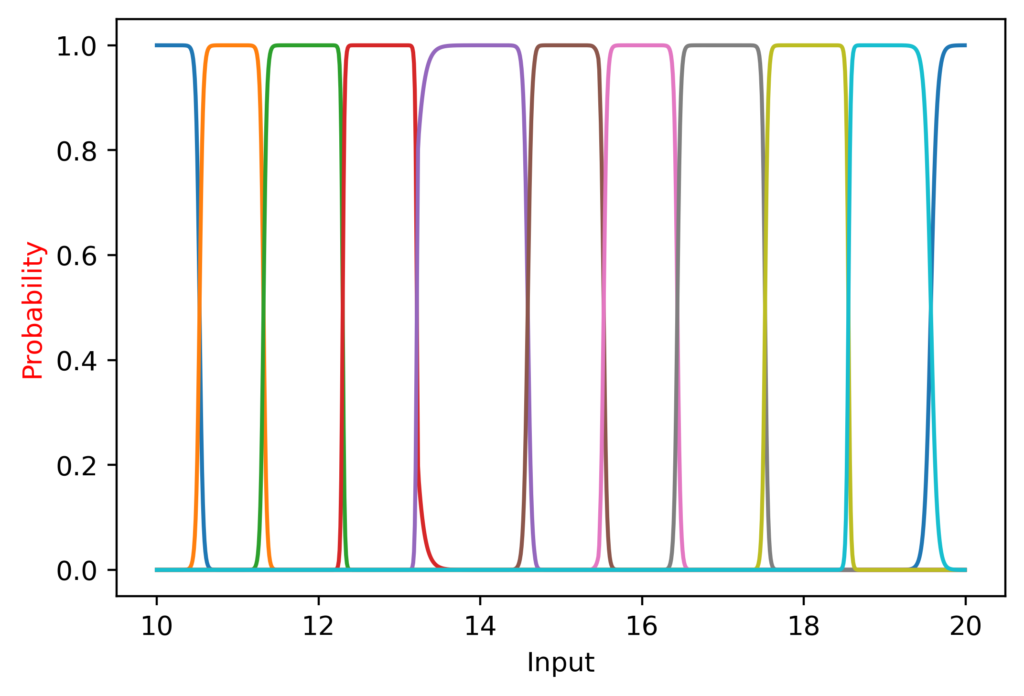
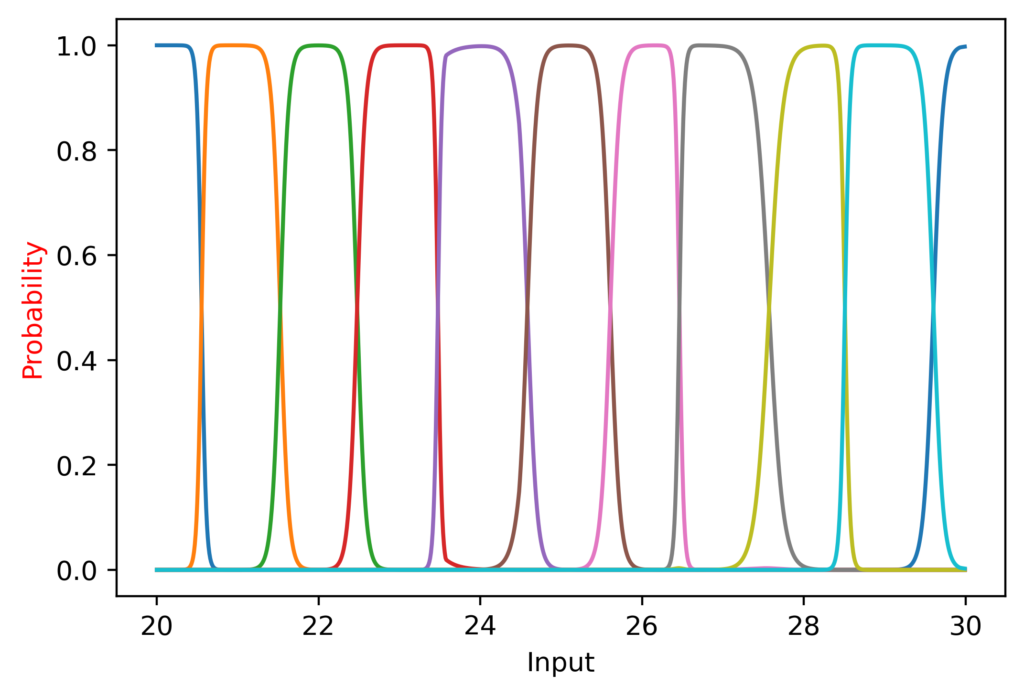
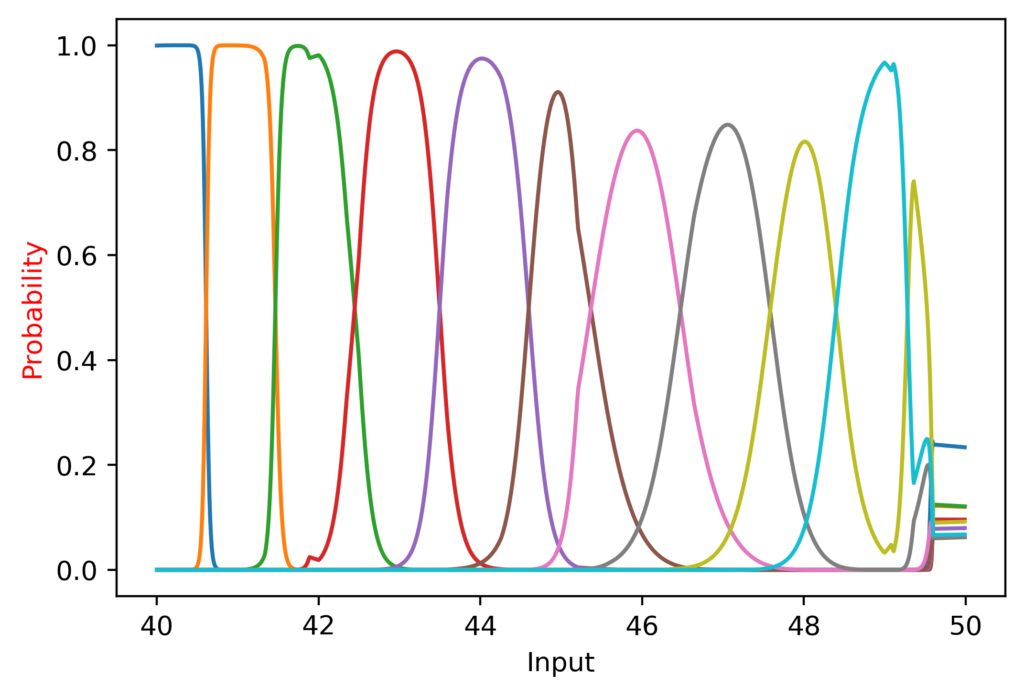
The full links are here [WIP], and the results were fairly expected: training longer and with a sufficient amount of layers gave the best results (and too many layers led to worse results – although this likely would be solved with longer training). One thing that continued to occur is that predictions for lower input values were more accurate, although there were some slight inconsistencies as seen here:
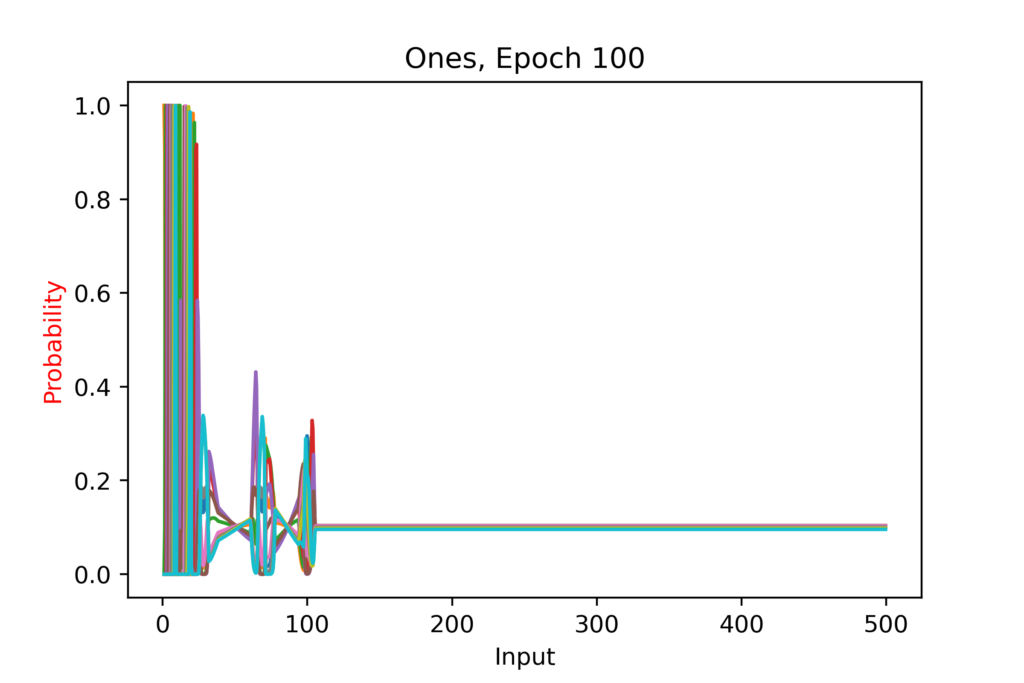
Notice how while lower values trained first, occassionally it would skip sections? This points to a probability that lower numbers train first rather than an absolute.
I have a few theories on why this might occur:
- The model trains and updates the model in a sequential fashion, and so values tend to get updated towards the first in the sequence (<5% chance; I believe the loss function is calculated all at once, and the loss for each node output is not calculated individually).
- Lower numbers have a higher relative difference (2 is twice 1; 102 is 1% higher than 101), and so there is a higher gradient when “fixing” lower numbers. The result is that lower numbers train faster than higher numbers, and the weights get “used up” accounting for lower numbers before higher numbers can get trained. (60%; I think this is likely)
- The relative difference is smaller at higher numbers, so the optimizer might “jump over” optimal values and have difficulty converging. Very similar to 2, and I’m not sure they are actually distinct theories.
- A quirk of the optimizer (similar to 1, but I don’t understand optimizers as well, so my uncertainty is higher. 10%)
- Something else I am not thinking of. Email me if you have an idea! (25%)
My last idea, that this all has been building up towards, is that model (ones, tens, hundreds) should be more accurate if it knows the output of the model above it. So tens should be more accurate if it knows what the hundreds digit is. The reasoning being that for input 418, if the hundreds digit is 4, the tens digit can subtract 4*100 and get just 18, which is easier to predict on. That leads to this model:
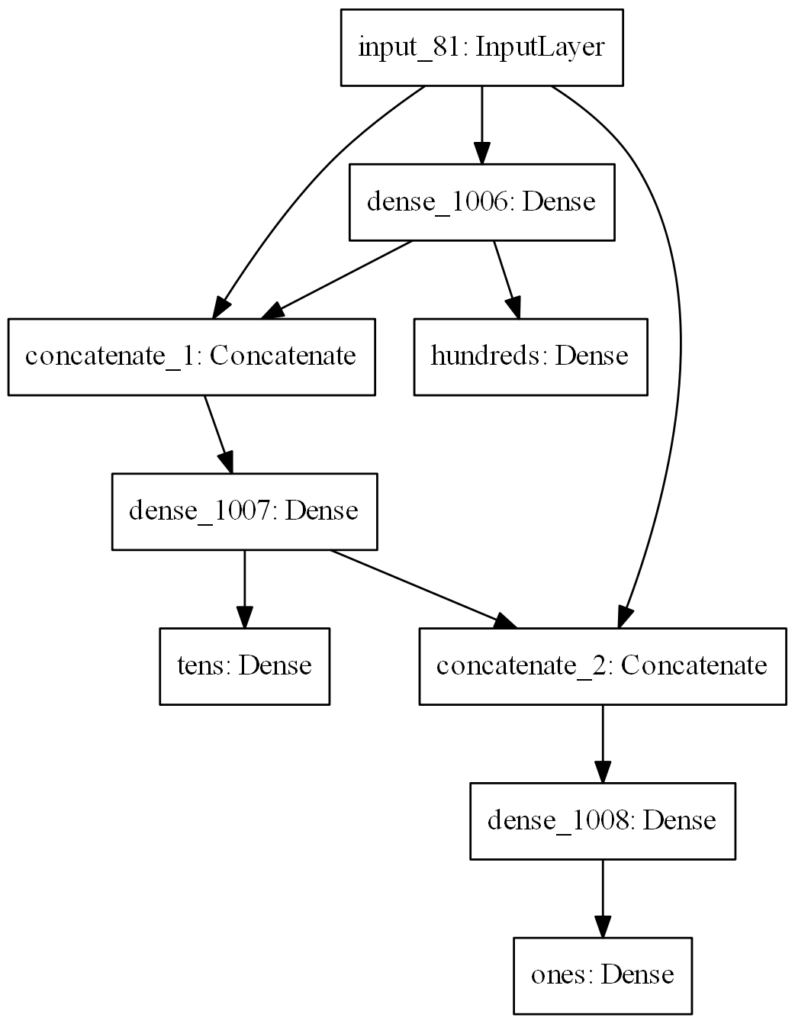
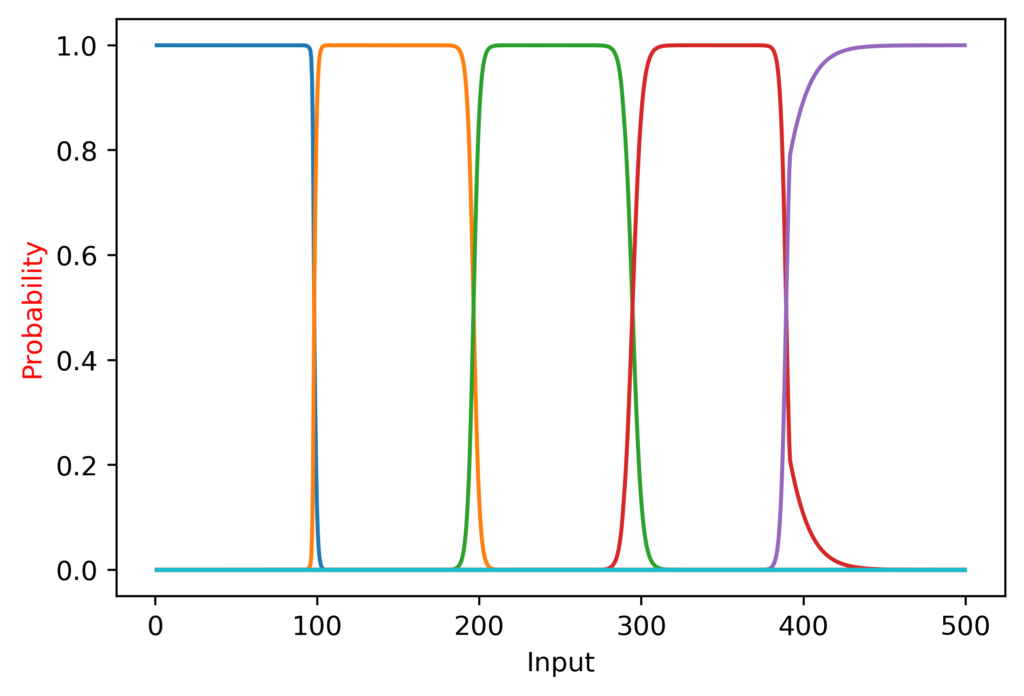
So I compiled the model, trained it, and it didn’t perform as well as I would have thought – worse, even, than the previous model (where each output did not feed into the next. I suspected this was because all outputs were training simultaneously – as in, the tens was still training while the hundreds output was nonsense. I decided to train in stages, with the hundreds by itself first, then the tens, and then the ones, to see how it performed. I worried that this would lead to tens training screwing up the hundreds weights, but decided to play around with it and see if it actually was a problem.
As it turns out, this is exactly what happened. The hundreds trained accurately initially, and the peaks were often shifted after training tens. I tried training hundreds first, then training hundreds at tens together; this kept the peaks in the right place, but softened the edges, as seen here:
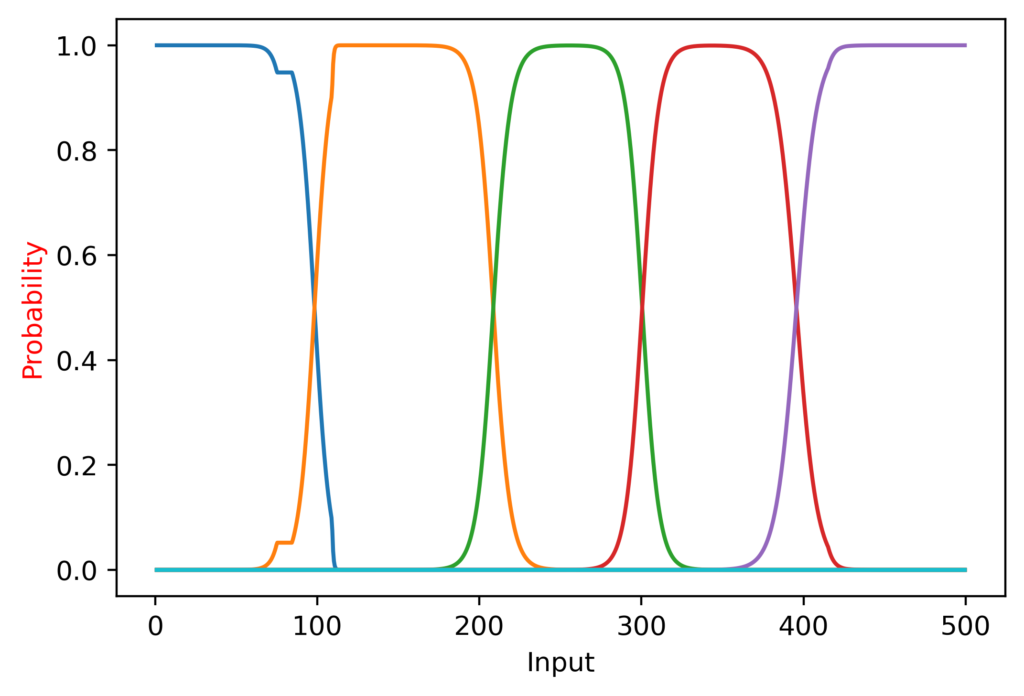
However, I made another discovery that really surprised me. I expected the tens digit prediction to be most accurate when hundreds knew exactly what it was (e.g. tens would be more accurate at 330-370 than 280-320, because the hundreds is less accurate on the latter interval). Instead, the opposite was true:
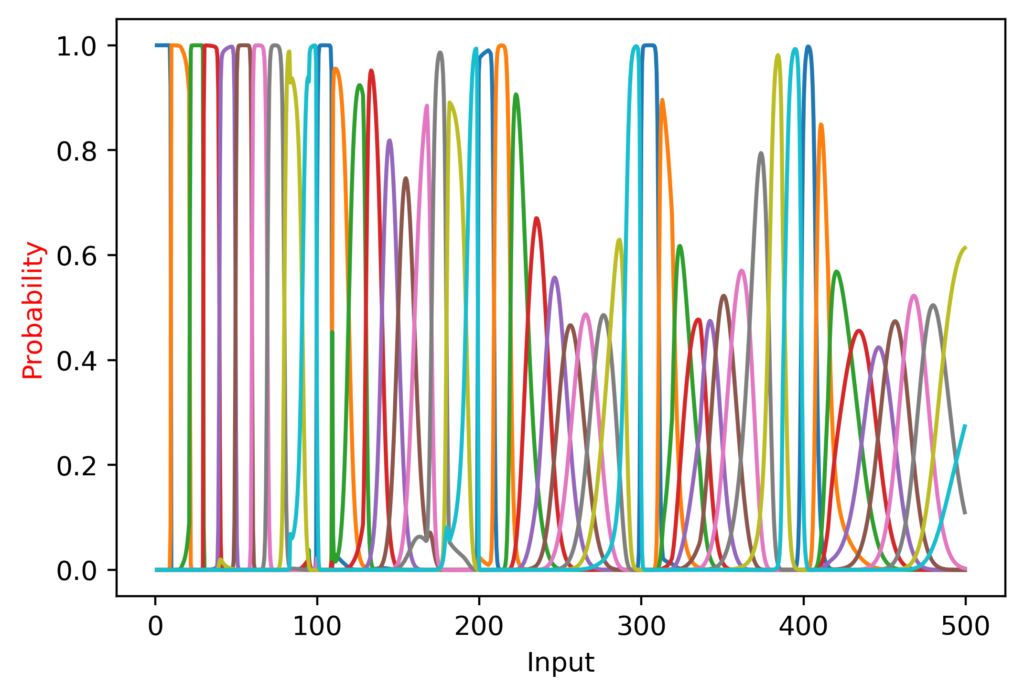
I realized why: When the hundreds is transitioning between predictions, this gives a very clear signal to tens that it is in the intermediary range; that is, when hundreds has a prediction of 0.5 for “2” and 0.5 for “3”, the tens digit knows it is at ~300 exactly, instead of being on the range of 320 to 380 when the hundreds predicts “3” only.
This is one of those areas where ML makes inferences differently than a human: it finds patterns, where a human uses logic and more precise calculations.
I may come back to this problem when I have new ideas in model architecture I’d like to experiment with.